Рассмотрим некоторые моменты, которые помогут нам быстро вспомнить материал 6 класса и успешно подготовиться к первому заданию ОГЭ.
Основное свойство дроби звучит так:
Если числитель и знаменатель обыкновенной дроби умножить или разделить на одно и то же отличное от нуля число, то получится равная ей дробь.
Основное свойство дроби распространяется и на дробное выражение – частное двух выражений, в котором знак деления заменен чертой дроби. Таким образом, дробное выражение можно без его изменения делить или умножать на одно и то же не равное нулю число или выражение.
Внимание: равенство или неравенство нулю любого числа совершенно очевидно. Однако с выражением, зависящем от каких-либо переменных, это не всегда так. Поэтому, домножая дробь на выражение, надо дополнительно исключить из рассмотрения те значения переменных, при которых оно обращается в нуль.
Рассматриваемое свойство, действительно, является основным – самым важным. Оно помогает нам во многих разных ситуациях. Благодаря нему мы можем выполнять следующие действия, которые мы пока рассмотрим на примере обыкновенных дробей.
1. Сокращение дроби
Сокращение дроби – это деление числителя и знаменателя на любой их общий делитель. Если дробь смешанная, то эта процедура проводится с её дробной частью. Например:
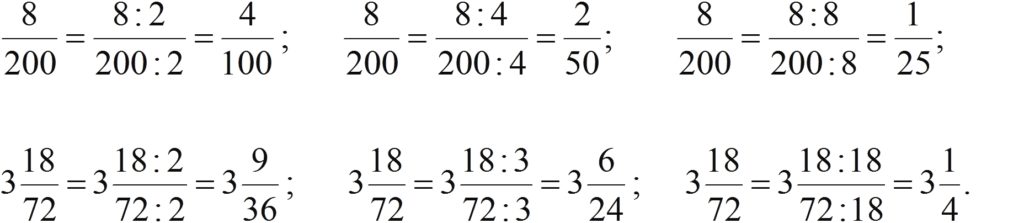
Часто при записи окончательного ответа нужно представить обыкновенную дробь в виде несократимой (числитель и знаменатель – взаимно простые числа). Алгоритм таков: находим наибольший общий делитель (НОД) числителя и знаменателя и делим на него и числитель, и знаменатель. Например:
Обратите внимание: во втором примере числитель одной из дробей (23) – простое число.
2. Приведение дробей к общему знаменателю
Для этого числители и знаменатели двух или более дробей домножаются так, чтобы знаменатели этих дробей стали наименьшими равными. Алгоритм действия: вначале находится наименьшее общее кратное (НОК) знаменателей всех дробей, которое и становится «новым» (общим) знаменателем. Затем числитель и знаменатель каждой дроби домножается на так называемый дополнительный множитель: частное «нового» и «старого» знаменателя дроби.
Например, приведем к общему знаменателю следующие дроби: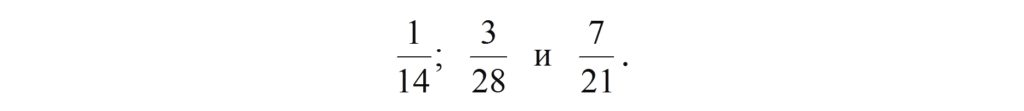 
Найдем наименьшее общее кратное их знаменателей: 
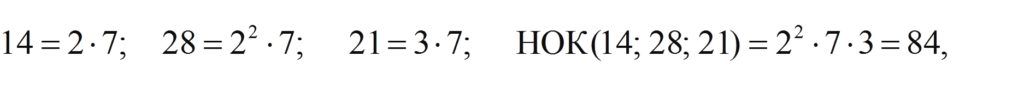и дополнительные множители, т. е. те множители, на которые мы будем домножать числитель и знаменатель дроби. Для первой дроби это 84:14 = 6; для второй дроби – 84:28 = 3 и для третьей дроби – 84:21 = 4.
Итак:
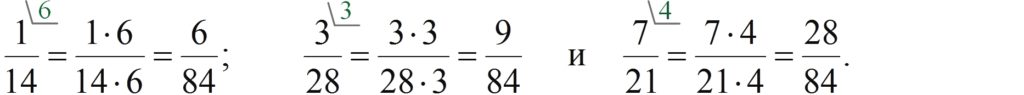
Приведение к общему знаменателю часто необходимо при сравнении дробей, а также при их сложении или вычитании.
3. Перевод обыкновенной дроби в десятичную
Сразу отметим, что в виде конечной десятичной дроби можно представить лишь ту несократимую дробь, знаменатель которой делится только на степени двойки и степени пятерки, т. е. представим в виде $$2^{n}\cdot5^{k}$$Для получения в знаменателе степени числа десять надо домножить этот знаменатель на «недостающие» двойки или пятерки. Если число смешанное, работаем только с дробной частью: целая часть «наследуется» десятичной дробью без всяких изменений. Например:
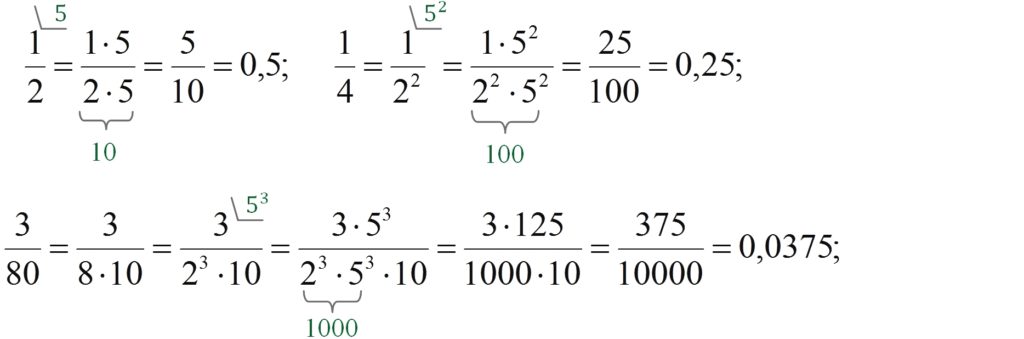
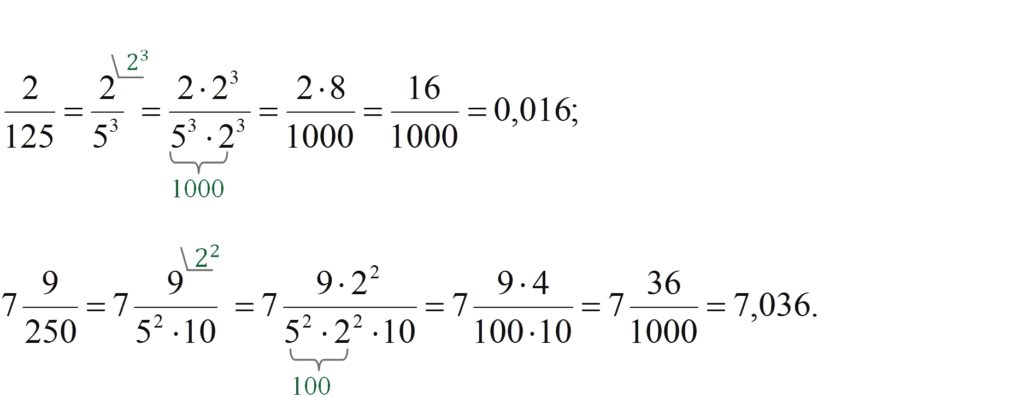
Умение переводить обыкновенные дроби в десятичные на ОГЭ по математике незаменимо: как известно, пока все ответы в тестовой части принимаются только в такой форме.